QUESTION: Calculate the freezing point of the dead sea?


Water density: 1.24 g/mL
satellite view

Map of the concentration of salt
in the ocean in g / 1000 g sea water
DATA and INFORMATION
Ion concentration in the water
ion concentration mg / L sea water
Cl- 224000
Mg2+ 44000
Na+ 40100
Ca2+ 17200
K+ 7650
Br- 5300
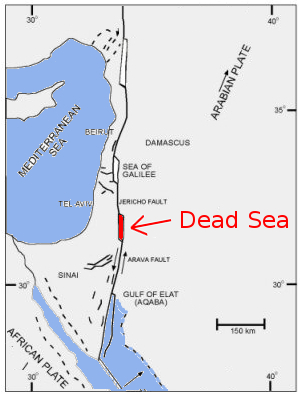
Other information
  • Lowest place on earth: - 480 m vs. ocean level.
  • Evaporation of the lake's waters: 1,4 m a year (estimated)
  • The salt concentration is 10 time higher than the one of the ocean
  • The density of the water is 1.24 g/mL
  • Water temperature at the lowest level of the Dead Sea: 22 °C (constant)
Assumption No ion pairing (which is probably wrong a those concentrations!)
Sources Dead Sea research center,  www.britannica.com ,  http:wikipedia.org ,  www.nasa.gov,
SOLUTION
The freezing point depression equation will be use for this problem
The total concentrations of all the ions (in molal: mol solute /kg solvent) has to be calculated
The following sample calculations are for the chloride ion. The calculation is the same for all the other ions
mass of Cl- in 1 L solution
  Mass of Cl- =   224000 mg
1 L
 X   1 g
1000 mg
  x 1000 L = 224 g    
 
Mass of 1 L of solution
  1 L solution = 1000. mL X  1.24 g
1 mL
  = 1240 g    
 
Total mass of all the ions in 1240 g solution
ion concentration (mg / L sea water) mass (g)
Cl- 224000 224
Mg2+ 44000 44.0
Na+ 40100 40.1
Ca2+ 17200 17.2
K+ 7650 7.65
Br- 5300 5.30
Total 338
Mass of solvent in 1 L solution mass water (solvent) = 1240 g solution - 338 g solute (total) = 902 g solvent (0.902 kg solvent)
Mole of Cl- in 1 L solution
  Mole of Cl- = 224 g X  1 mol
35.45 g
  = 6.319 mol    
 
Molality of Cl-
  m =   6.319 mol
0.902 kg
  = 7.01 molal  (3 S.F.)  
 
Total concentration of particles
ion concentration (mg / L sea water) concentration (molal)
Cl- 224000 7.01
Mg2+ 44000 2.01
Na+ 40100 1.93
Ca2+ 17200 0.476
K+ 7650 0.217
Br- 5300 0.074
Total molality of particles (ions) 11.7
Freezing point depression Tf (pure water) = 0.00 °C
Kf (water) = 1.86 °C.kg.mol-1

ΔTf = i Kf (solvent) m

Note: here, m = molality of all the particles, then the van't Hoff factor ( i ) = 1. ΔTf = Kf (water) m   Finally: ΔTf = 1.86 °C.kg.mol-1 x 11.7 mol.kg-1 = 21.8 °C
Since the freezing point of pure water = 0 °C,then, the freezing point of the Dead sea = -21.8 °C
ANSWER: -21.8 °C       (Actual value -21.1 °C) ,